多项式长除法是怎么算的？原理是什么？我看长除法的过程都看不懂。

多项式长除法是怎么算的？原理是什么？我看长除法的过程都看不懂。

把被除式、除式按某个字母作降幂排列，并把所缺的项用零补齐；用被除式的第一项除以除式第一项，得到商式的第一项；用商式的第一项去乘除式，把积写在被除式下面（同类项对齐），消去相等项，把不相等的项结合起来。

把减得的差当作新的被除式，再按照上面的方法继续演算，直到余式为零或余式的次数低于除式的次数时为止，被除式=除式×商式+余式。若余式为零，说明这个多项式能被另一个多项式整除。

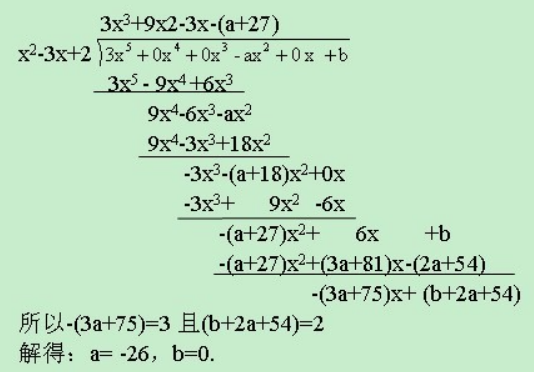
扩展资料

计算

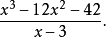
1、把被除式、除式按某个字母作降幂排列，缺项补零，写成以下形式：

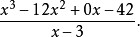
然后商和余数可以这样计算：

2、用分子的第一项除以分母的最高次项（即次数最高的项，此处为x），得到首商，写在横线之上（x³÷x=x²）。将分母乘以首商，乘积写在分子前两项之下（同类项对齐） x²×(x−3) =x³−3x²。

3、从分子的相应项中减去刚得到的乘积（消去相等项，把不相等的项结合起来），得到第一余式，写在下面。然后，将分子的下一项“拿下来”。

4、把第一余式当作新的被除式，重复前三步，得到次商与第二余式（直到余式为零或余式的次数低于除式的次数时为止，被除式=除式×商式+余式 ）。

5、重复第四步，得到三商与第三余式。余式小于除式次数，运算结束。