求阴影面积

求阴影面积

给一个同类问题，供参考。

已知正方形边长为2R，求阴影部分面积 100

如图

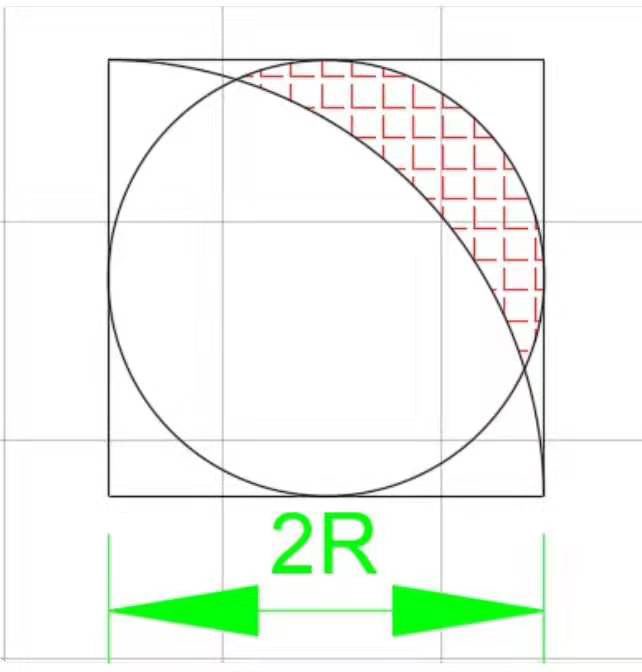
请点击输入图片描述

解：设正方形ABCD的边长为2R,分别以AB,AD为x,y轴建立直角坐标系，

圆A的方程是x^2+y^2=4R^2,①

正方形的内切圆方程是(x-R)^2+(y-R)^2=R^2,②

①-②，得2R(x+y)=5R^2,y=5R/2-x,③

把③代入①，得2x^2-5Rx+9R^2/4=0,

解得x1=(5-√7)R/4,x2=(5+√7)R/4.

阴影部分面积分两部分计算：

I1=∫<x1,x2>[R+√（2Rx-x^2）-√(4R^2-x^2)]dx

={Rx+(x-R)/2*√（2Rx-x^2）+R^2/2*arcsin[(x-R)/R]

-x/2*√(4R^2-x^2)-2R^2*arcsin[x/(2R)}|<x1,x2>

=R^2{√7/2+（1+√7）/8*(√7-1)/4-(1-√7)/8*(1+√7)/4+(1/2)[arcsin((1+√7)/4)-arcsin((1-√7)/4)]-(5+√7)/8*(5-√7)/4+(5-√7)/8*(5+√7)/4-2[arcsin((5+√7)/8)-arcsin((5-√7)/8)]}

=R^2{√7/2+3/8+(1/2)[arcsin((1+√7)/4)-arcsin((1-√7)/4)]

-2arcsin((5+√7)/8)+2arcsin((5-√7)/8)}，

I2=∫<x2,2R>2√(2Rx-x^2)dx

={(x-R)√（2Rx-x^2）+R^2*arcsin[(x-R)/R]}|<x2,2R>

=R^2{-(1+√7)/4*(√7-1）/4+π/2-arcsin((1+√7)/4)}

=R^2{-3/8+π/2-arcsin((1+√7)/4)}，

所以所求阴影部分面积I=I1+I2

=R^2{√7/2+π/2-(1/2)[arcsin((1+√7)/4)+arcsin((1-√7)/4)]

-2arcsin((5+√7)/8)+2arcsin((5-√7)/8)}，

sin[arcsin((1+√7)/4)+arcsin((1-√7)/4)]

=(1+√7)/4*(√7+1）/4+(√7-1)/4*(1-√7)/4

=√7/4，

所以[arcsin((1+√7)/4)+arcsin((1-√7)/4)]=arcsin(√7/4），

sin{arcsin((5+√7)/8)-arcsin((5-√7)/8)]

=(5+√7)^2/64-(5-√7)^2/64=5√7/16，

所以arcsin((5+√7)/8)-arcsin((5-√7)/8)=arcsin(5√7/16),

所以I=R^2{√7/2+π/2-(1/2)arcsin(√7/4)-2arcsin(5√7/16)}.