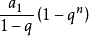数列的通项公式怎么求？

数列的通项公式怎么求？

1. 等差数列

对于一个数列{ an }，如果任意相邻两项之差为一个常数，那么该数列为等差数列，且称这一定值差为公差，记为 d ；从第一项 a1到第n项 an的总和，记为Sn 。

那么 ， 通项公式为

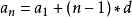
其求法很重要，利用了“叠加原理”的思想：

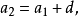
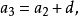
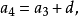
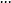
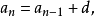
将以上 n-1 个式子相加， 便会接连消去很多相关的项 ，最终等式左边余下an ,而右边则余下a1和 n-1 个d,如此便得到上述通项公式,此外， 数列前 n 项的和

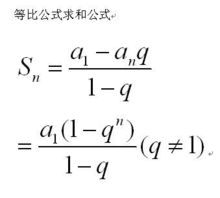
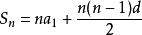
其具体推导方式较简单，可用以上类似的叠加的方法，也可以采取迭代的方法，在此，不再复述。值得说明的是，也即，前n项的和Sn 除以 n 后，便得到一个以a1 为首项，以 d /2 为公差的新数列，利用这一特点可以使很多涉及Sn的数列问题迎刃而解。

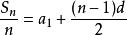
2. 等比数列

对于一个数列 {an}，如果任意相邻两项之商（即二者的比）为一个常数，那么该数列为等比数列，且称这一定值商为公比 q ；从第一项a1 到第n项an 的总和，记为Tn 。那么， 通项公式为

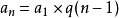
(即a1 乘以q 的 （n-1)次方，其推导为“连乘原理”的思想：

a2=a1 * q,

a3= a2 * q,

a4= a3 * q,

````````

an=an-1 * q,

将以上(n-1)项相乘，左右消去相应项后，左边余下an , 右边余下a1和(n-1)个q的乘积，也即得到了所述通项公式。此外， 当q=1时 该数列的前n项和

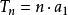
当q≠1时 该数列前n 项的和

 =
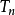