芝诺悖论有哪四个？

芝诺悖论有哪四个？

1、二分法悖论

一个人在到达目的地之前，要先走完路程的1/2，再走完剩下总路程的1/2，再走完剩下的1/2……按照这个要求可以无限循环的进行下去。因此有两种情况：①这个人根本没有出发；②只要他出发了，就永远到不了终点。（尽管离终点越来越近）

2、阿基里斯悖论

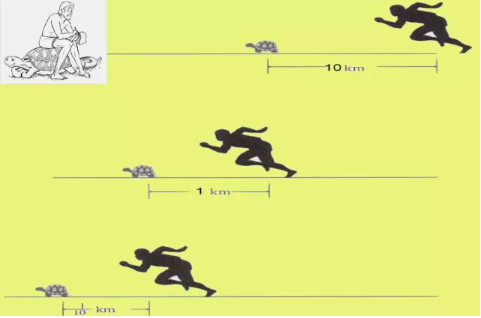
其实，这个悖论就是指这个有趣的故事——阿基里斯与乌龟赛跑。阿基里斯是古希腊神话中善跑的英雄。在他和乌龟的竞赛中，他速度为乌龟10倍，乌龟在前面100米跑，他在后面追，但他不可能追上乌龟。

3、飞矢不动

“飞矢不动”中的“矢”指的是弓箭中的箭。正常的射箭，任何人都知道，只要箭离了弦，就能飞出去，经过一段空间运动后，到达另一个位置。

然而，芝诺认为：如果我们截取“飞矢”的每一个瞬间，它在空中都是“静止”的。既然每一个瞬间都是静止的，所有的瞬间加起来也应该是静止的，因此，“飞矢”是“不动”的。

4、游行队伍悖论

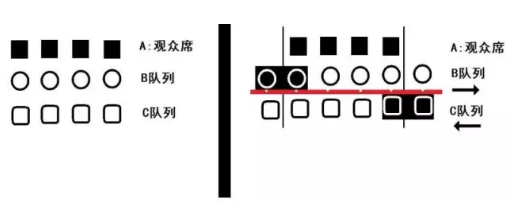
假设在运动场上，在一瞬间（一个最小时间单位）里，相对于观众席A，队列B、C分别各向右和左移动一个距离单位。

而此时，相对于B，C移动了两个距离单位。芝诺认为，既然队列可以在一瞬间（一个最小时间单位）里移动一个距离单位，也可以在半个最小时间单位里移动一个距离单位，那么，半个时间单位就等于一个时间单位。

扩展资料

亚里士多德对芝诺悖论作出了这样的解释：

对于第一、三个悖论，他认为只要假设时间是也是无限不可分的，那么每一个时间点对应一个空间点，就能在无限不可分的一段时间里跨过一段无限不可分的空间。

对于第二个悖论，他认为：当追赶者与被追者之间的距离越来越小时，追赶所需的时间也越来越小。无限个越来越小的数加起来的和是有限的，所以可以在有限的时间追上。（然而并不严谨）

而对于阿基里斯悖论，阿基米德发现了一种类似于几何级数求和的方法，而问题中所需的时间是成倍递减的，这正是一个典型的几何级数，由此可知阿基里斯追上乌龟的总时间是一个有限值。