圆周角定理的定理证明
的有关信息介绍如下:圆周角定理:一条弧所对圆周角等于它所对圆心角的一半
证明:
已知在⊙O中,∠BOC与圆周角∠BAC同对弧BC,求证:∠BOC=2∠BAC.
证明:
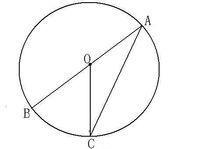
情况1:如图1,当圆心O在∠BAC的一边上时,即A、O、B在同一直线上时:
∵OA、OC是半径
解:∴OA=OC
∴∠BAC=∠ACO(等边对等角)
∵∠BOC是△AOC的外角
∴∠BOC=∠BAC+∠ACO=2∠BAC
图1
情况2:
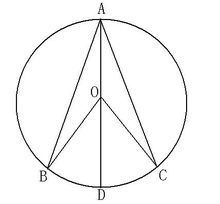
如图2,,当圆心O在∠BAC的内部时:
连接AO,并延长AO交⊙O于D
∵OA、OB、OC是半径
解:∴OA=OB=OC
∴∠BAD=∠ABO,∠CAD=∠ACO(等边对等角)
∵∠BOD、∠COD分别是△AOB、△AOC的外角
∴∠BOD=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和)
∠COD=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和)
∴∠BOC=∠BOD+∠COD=2(∠BAD+∠CAD)=2∠BAC
图2
情况3:
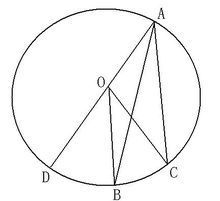
如图3,当圆心O在∠BAC的外部时:
连接AO,并延长AO交⊙O于D连接OA,OB。
解:∵OA、OB、OC、是半径
∴OA=OB=OC
∴∠BAD=∠ABO(等边对等角),∠CAD=∠ACO(OA=OC)
∵∠DOB、∠DOC分别是△AOB、△AOC的外角
∴∠DOB=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和)
∠DOC=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和)
∴∠BOC=∠DOC-∠DOB=2(∠CAD-∠BAD)=2∠BAC
从而得证:∠BOC=2∠BAC.
图3
扩展资料:
定理推论
1.一条弧所对的圆周角等于它所对的圆心角的一半;
2.圆周角的度数等于它所对的弧度数的一半;
3.在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等。
4.半圆(直径)所对的圆周角是直角。
5.90°的圆周角所对的弦是直径。
6.等弧对相等的圆周角。(因为相等的弧只有一个圆心角)
注意:在圆中,同一条弦所对的圆周角有无数个。



