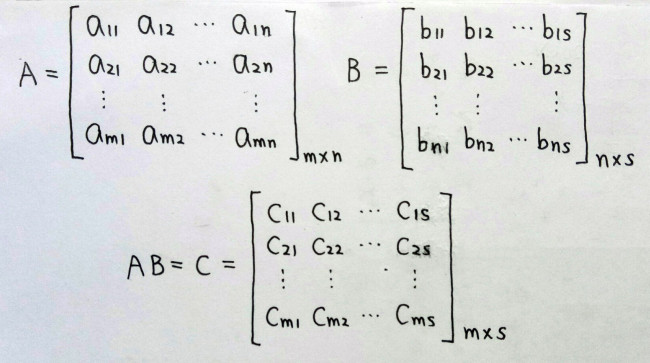什么是逆矩阵
的有关信息介绍如下:
设A是数域上的一个n阶矩阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=E ,则我们称B是A的逆矩阵,而A则被称为可逆矩阵。注:E为单位矩阵。逆矩阵,或可逆是线性代数中最重要的内容。
1、下列命题等价:
1)A为n阶可逆矩阵
2)A是非奇异的。
3)A是满秩的。
4)A是行满秩的。
5)A是列满秩的。
6)方程组AX=0仅有零解
7)方程组AX=B仅有唯一解。
8)A的行向量组线性无关。
9)A的列向量组线性无关。
10)A的任何特征值均非零。
2、可逆的重要性体现在:
AB=C 表示B线性变换到 C, B与C是等价矩阵。同秩,同可逆或不可逆。是以B的列向量与C的列向量为基构成的向量空间为相同的空间。
扩展资料
逆矩阵性质定理
可逆矩阵一定是方阵。
如果矩阵A是可逆的,其逆矩阵是唯一的。
A的逆矩阵的逆矩阵还是A。记作(A-1)-1=A。
可逆矩阵A的转置矩阵AT也可逆,并且(AT)-1=(A-1)T (转置的逆等于逆的转置)
若矩阵A可逆,则矩阵A满足消去律。即AB=O(或BA=O),则B=O,AB=AC(或BA=CA),则B=C。
两个可逆矩阵的乘积依然可逆。
矩阵可逆当且仅当它是满秩矩阵。