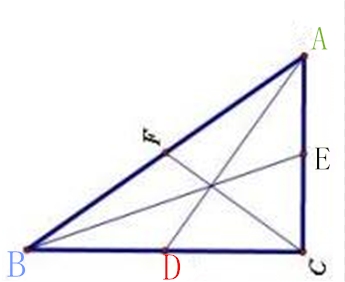
Simone如图，在RT三角形ABC中，∠ACB=90°，AD,BE,CF分别是三边上的中线。
的有关信息介绍如下：27.（本题满分8分）如图，在RT△ABC中，∠ACB=90°，AD,BE,CF分别是三边上的中线。
（1）若AC=1,BC=√2。求证：AD²+CF²=BE²；
（2）是否存在这样的RT△ABC，使得它三边上的中线AD、BE、CF的长恰好是一组勾股数？请说明理由。
答案：
AD²=AC²+CD²=AC²+(1/2BC)²=1+1/2=3/2
CF²=(1/2AB)²=1/4AB²=1/4(AC²+BC²)=3/4
BE²=BC²+(1/2AC)²=9/4
故AD²+CF²=BE²
由勾股定理A²+B²=C²，由本题前面得证
AD²+CF²=BE²
可知存在这样的RT△ABC
