t检验与f检验的区别？

t检验与f检验的区别？

1、定义

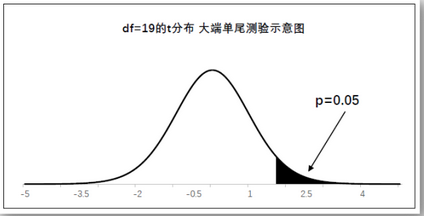
t检验，亦称student t检验（Student's t test），主要用于样本含量较小（例如n < 30），总体标准差σ未知的正态分布。是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。它与f检验、卡方检验并列。

f检验（F-test），最常用的别名叫做联合假设检验，此外也称方差比率检验、方差齐性检验。是一种在零假设之下，统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型，以判断该模型中的全部或一部分参数是否适合用来估计母体。

2、适用条件

t检验的适用条件：已知一个总体均数；可得到一个样本均数及该样本标准差；样本来自正态或近似正态总体。

f检验的适用条件：假设一系列服从正态分布的母体，都有相同的标准差；假设一个回归模型很好地符合其数据集要求。

扩展资料：

t检验的注意事项：

1、选用的检验方法必须符合其适用条件；

2、区分单侧检验和双侧检验。

3、假设检验的结论不能绝对化。

4、正确理解P值与差别有无统计学意义。

f检验的注意事项：

1、f检验对于数据的正态性非常敏感，因此在检验方差齐性的时候，Levene检验, Bartlett检验或者Brown–Forsythe检验的稳健性都要优于f检验。 

2、f检验还可以用于三组或者多组之间的均值比较，但是如果被检验的数据无法满足均是正态分布的条件时，该数据的稳健型会大打折扣，特别是当显著性水平比较低时。

参考资料来源：百度百科-T检验

百度百科-F检验