什么是代数余子式？

什么是代数余子式？

代数余子式：

在n阶行列式中，把元素aₒₑi所在的第o行和第e列划去后，留下来的n-1阶行列式叫做元素aₒₑi的余子式，记作Mₒₑ，将余子式Mₒₑ再乘以-1的o+e次幂记为Aₒₑ，Aₒₑ叫做元素aₒₑ的代数余子式。

一个元素aₒₑi的代数余子式与该元素本身没什么关系，只与该元素的位置有关。

例子：

例1 在五阶行列式 

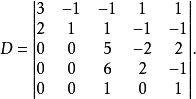中，划定第二行、四行和第二列、三列，就可以确定D的一个二阶子行列式

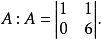A的相应的余子式M为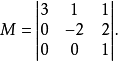：子行列式A的相应的代数余子式为：

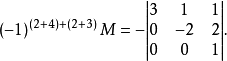
扩展资料：

代数余子式求和

带有代数符号的余子式称为代数余子式，计算元素的代数余子式时，首先要注意不要漏掉代数余子式所带的代数符号  。

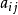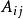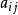计算某一行(或列)的元素代数余子式的线性组合的值时，尽管直接求出每个代数余子式的值，再求和也是可行的，但一般不用此法，其原因是计算量太大，注意到行列式D中元素  的代数余子式  与  的值无关。

仅与其所在位置有关，利用这一点，可将D的某一行(或列)元素的代数余子式的线性组合表示为一个行列式，而构造这一行列式是不难的，只需将其线性组合的系数替代D的该行(或该列)元素，所得的行列式 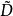 就是所要构造的行列式，再应用下述行列式的展开定理，即命题1和命题2，就可求得  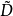的值。

命题 1 n阶行列式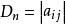  

等于它的任一行(列)的所有元素与其对应的代数余子式的乘积之和：

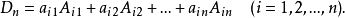
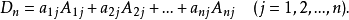
命题2 n阶行列式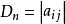  

的任一行(列)的元素与另一行(列)对应元素的代数余子式乘积之和等于零：

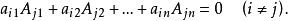
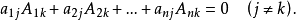
参考资料：百度百科---代数余子式