Simone特征多项式怎么求？
的有关信息介绍如下：解法：
1、把|λE-A|的各行（或各列）加起来，若相等，则把相等的部分提出来（一次因式）后，剩下的部分是二次多项式，肯定可以分解因式。
2、把|λE-A|的某一行（或某一列）中不含λ的两个元素之一化为零，往往会出现公因子，提出来，剩下的又是一二次多项式。
3、试根法分解因式。
性质：
当A为上三角矩阵（或下三角矩阵）时，
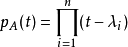，其中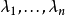 
是主对角线上的元素。对于二阶方阵，特征多项式能表为
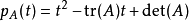。一般而言，若 
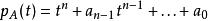，则
。
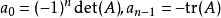此外：
（1）特征多项式在基变更下不变：若存在可逆方阵 C使得
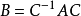，则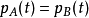 
。
（2）对任意两方阵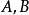 
，有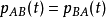 
。一般而言，若A为 
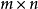矩阵，B 为 
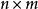矩阵（设 
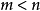），则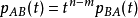 
。
（3）凯莱-哈密顿定理：
。
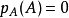参考资料：百度百科-特征多项式
