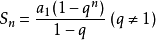等比数列和等差数列的递推公式
的有关信息介绍如下:
我也从网上找个资料吧。等差数列:设有一个等差数列a1,a2,a3,...an,这个数列的每一项加一个定数都等于后一项,这个定数就叫数列的公差,设公差是d,数列也可表示为a1,a1+d,a1+2d,....a1+(n-1)d,可见此数列的通项公式就是an=a1+(n-1)d求此数列前n项的和:细观察可发现,等差数列的第一项加最后一项正好等于第二项加倒数第二项,第三项加倒数第三项也等于第一项加最后一项,....所以可得Sn=n(a1+an)/2,Sn表示数列前n项的和,如果把an=a1+(n-1)d代入,还可表示为Sn=n[2a1+(n-1)d]/2等比数列:设有一个等比数列a1,a2,a3,...an,这个数列(从第二项起)每一项除以前一项都等于一个定数,这个定数就叫数列的公比,设公比是q,数列也可表示为a1,a1q,a1q²,....a1q^(n-1),可见此数列的通项公式就是an=a1*q^(n-1)求此数列前n项的和:设Sn=a1+a1q+a1q²+....+a1q^(n-1),(1)将等式两边同乘以q,可得q*Sn=a1q+a1q²+a1q³+....+a1q^(n-1),a1q^n,(2)用(1)减(2),可得Sn(1-q)=a1-a1q^n就是Sn=a1(1-q^n)/(1-q)这就是等比数列前n项和的公式.