设集合A={1,2,3,4,6,8,12}, R是A上的整除关系,(1)画出偏序集(A, R)的哈斯图;
的有关信息介绍如下:写出R的集合表示,先去掉所有的<a.a>形式的元素,再破坏传递性,若<a,b>,<b,c>,a,c>都在R中,则去掉<a,c>,最后把剩下的元素画图,<a,b>对应的边的始点a在下,终点b在上,这样得到的图就是哈斯图。
最大元素就是在子集(例题中指B={2,3,5})中处于最高层且每个元素通过图中路径都可以找到且上面没有元素。最小元素就是在子集中处于最低层且每个元素通过图中路径都可以找到且下面没有元素。极大元素就是在子集中的上面没有元素,极小元素就是在子集中的下面没有元素。
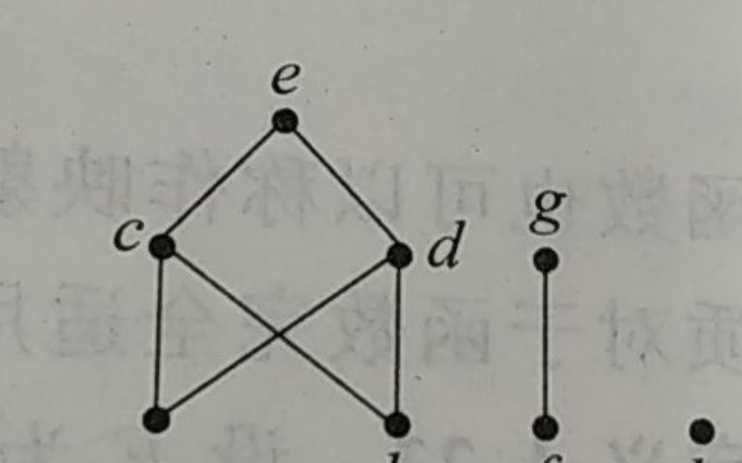
扩展资料:
偏序集注意事项:
对任意的a∈A,(a,a)∈P,若(a,b)∈P且(b,a)∈P,则a=b。
若(a,b)∈P,(b,c)∈P,则(a,c)∈P,则称P是A上的一个偏序关系。带偏序关系的集合A称为偏序集或半序集。
实数集上的小于等于关系是一个偏序关系,设S是集合,P(S)是S的所有子集构成的集合,定义P(S)中两个元素A≤B当且仅当A是B的子集,即A包含于B,则P(S)在这个关系下成为偏序集。
设N是正整数集,定义m≤n当且仅当m能整除n,不难验证这是一个偏序关系。注意不同于N上的自然序关系。
参考资料来源:百度百科-偏序集
参考资料来源:百度百科-哈斯图



