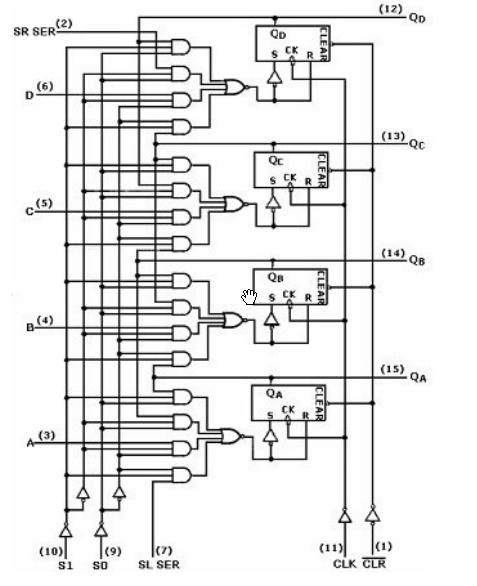
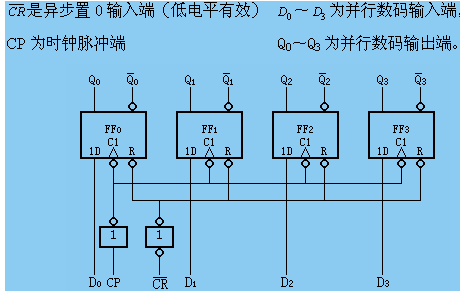
反馈移位寄存器的反馈移位寄存器的性质

反馈移位寄存器的反馈移位寄存器的性质

反馈函数f（a1,a2,a3,…an）为n元布尔函数。在时钟脉冲时，如果反馈移位寄存器的状态为si=(ai,…..ai+n-1)则

ai+n=f(ai,ai+1,...,ai+n-1), (2.1)

这个ai+n 又是移位寄存器的输入。在ai+n的驱动下，移位寄存器的各个数据向前推进一位，使状态变为si+1=(ai+1,…..ai+n)，同时，整个移位寄存器的输出为ai。由此得到的一系列数据：a1,a2,a3,…,an,…。该序列称为满足关系式（2.1）的一个反馈移位寄存器序列。

例如，线性反馈移位寄存器设f（a1,a2,a3,…an）=cna1⊕cn-1a2⊕….⊕c2an-1⊕c1an,

输出序列{ai}满足an+i= cnai⊕cn-1ai+1⊕….⊕c2an-2+i⊕c1an-1+i,其中i为非负整数。则该序列{ai}称为该反馈移位寄存器序列。 对于一个n级反馈移位寄存器来说，最多可以有2n个状态，对于一个线性反馈移位寄存器来说，全“0”状态不会转入其他状态，所以线性移位寄存器的序列的最长周期为2n-1。当n级线性移位寄存器产生的序列{ai}的周期为T=2n-1时，称{ai}为n级m序列。

已经证明，n级m序列{ai}具有以下性质：

在一个周期内，0，1出现次数分别为2n-1-1次和2n-1次；

在一个周期圈内，总游程（是指一个元素连续出现的次数）数为2n-1，对1≤i≤n-2，长度为i的游程有2n-i-1个，且0，1游程各半，长为n-1的0游程1个长为n的1游程1个；

所以可以看出，该序列满足Golomb的三个公设，具有良好的随机特性。

当反馈函数f（a1,a2,a3,…an）为非线性函数时，便构成非线性移位寄存器，其输出序列为非线性序列。输出序列的周期最大可达2n，并称周期达到最大值的非线性移位寄存器序列为m序列。在m序列的一个周期内，0和1的个数是相同的。在一个周期圈内，总游程数为2n-1，对1≤i≤n-2，长度为i的游程有2n-i-1个，且0，1游程各半，长为n-1的游程不存在，长度为n的0游程和1游程各一个。 对于线性反馈移位寄存器的输出序列{ai}满足递推关系an+i= cnai⊕cn-1ai+1⊕….⊕c2an-2+i⊕c1an-1+i,对于任意i≥1成立。其中c0=1，成为该线性移位寄存器或者该递推关系的特征多项式，当cn≠0时，线性移位寄存器是非奇异的，有时也称非奇异的线性移位寄存器是非退化的。