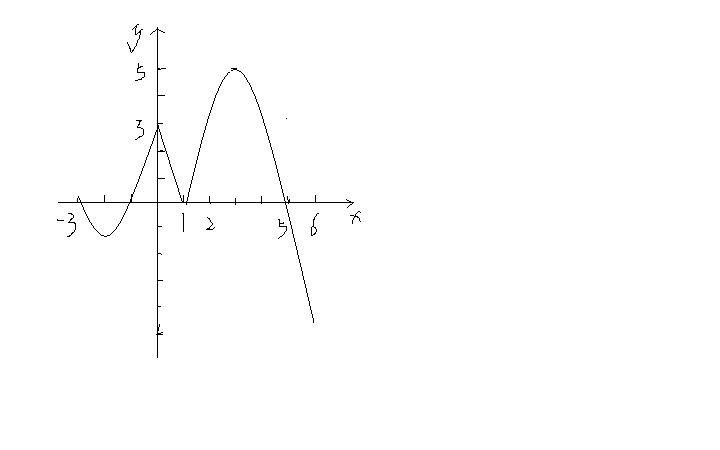
已知函数
的有关信息介绍如下:
导函数的定义:按上述求导数值的过程,当 取不同的值时,通常可求出相应不同的导数值,这样,通过对一个已知函数在不同点处求导数值,形成了一个新的量与量之间的对应关系,即导出了一个新的函数,这个函数称为已知函数的导函数(derived function),也简称为导数, 横向对比学习法:导数值和导函数都叫做导数,应该如何区分呢?可从 三个方面进行对比区分:第一:当导数问题指的是导函数时,结果是一个函数,提出问题时没有指定自变量的值;当导数指的是导数值时,求极限的结果是一个常数,提出问题时会附带指定一个自变量的值。第二:也可从记号中是否指出 x 等于几来区别。它们的关系是: 是 在点 处的函数值,前者仅仅是一个点的问题,后是是关于某区间上的问题。形式上还可从翻译符号进行区别。第三:可参看求导数值与求导函数的操作范例。典型范例2(求导函数操作三步曲) 第一步:在任一点 x 处给增量Δ x ,函数相应地有增量 第二步:作比 第三步:求极限 答案: 再作对比分析:将范例1与范例2进行对比发现,当 x=2 时,范例2中导函数的值等于 4,与范例1中求得的导数值一致。导数(derivative)亦名微商,由速度问题和切线问题抽象出来的数学概念。又称变化率。如一辆汽车在10小时内走了 600千米,它的平均速度是60千米/小时,但在实际行驶过程中,是有快慢变化的,不都是60千米/小时。为了较好地反映汽车在行驶过程中的快慢变化情况,可以缩短时间间隔,设汽车所在位置x与时间t的关系为x=f(t),那么汽车在由时刻t0变到t1这段时间内的平均速度是[f(t1)-f(t2)/t1-t2],当 t1与t0很接近时,汽车行驶的快慢变化就不会很大,平均速度就能较好地反映汽车在t0 到 t1这段时间内的运动变化情况 ,自然就把极限[f(t1)-f(t2)/t1-t2] 作为汽车在时刻t0的瞬时速度,这就是通常所说的速度。一般地,假设一元函数 y=f(x )在 x0点的附近(x0-a ,x0 +a)内有定义,当自变量的增量Δx= x-x0→0时函数增量 Δy=f(x)- f(x0)与自变量增量之比的极限存在且有限,就说函数f在x0点可导,称之为f在x0点的导数(或变化率)。若函数f在区间I 的每一点都可导,便得到一个以I为定义域的新函数,记作 f′,称之为f的导函数,简称为导数。函数y=f(x)在x0点的导数f′(x0)的几何意义:表示曲线l 在P0[x0,f(x0)] 点的切线斜率。导数是微积分中的重要概念。导数定义为,当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。在一个函数存在导数时,称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。物理学、几何学、经济学等学科中的一些重要概念都可以用导数来表示。如,导数可以表示运动物体的瞬时速度和加速度、可以表示曲线在一点的斜率、还可以表示经济学中的边际和弹性。求导数的方法(1)求函数y=f(x)在x0处导数的步骤: ① 求函数的增量Δy=f(x0+Δx)-f(x0) ② 求平均变化率 ③ 取极限,得导数。 (2)几种常见函数的导数公式: ① C'=0(C为常数); ② (xn)'=nxn-1 (n∈Q); ③ (sinx)'=cosx; ④ (cosx)'=-sinx; ⑤ (ex)'=ex; ⑥ (ax)'=axlna (3)导数的四则运算法则: ①(u±v)'=u'±v' ②(uv)'=u'v+uv' (4)复合函数的导数 复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以中间变量对自变量的导数。