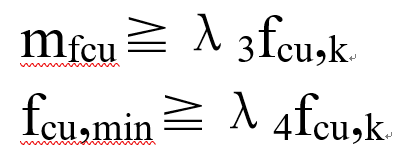什么是子集。什么是真子集。举例说明。

什么是子集。什么是真子集。举例说明。

子集：对于两个非空集合A与B,如果集合A的任何一个元素都是集合B的元素,我们就说 A ⊆ B(读作A含于B),或 B ⊇ A(读作B包含A),称集合A是集合B的子集.

真子集：如果A是B的子集,并且B中至少有一个元素不属于A,那么集合A叫做集合B的真子集.

举例说明

比如全集I为{1,2,3},

它的子集为{1}、{2}、{3}、{1,2}、{1,3}、{2,3}、{1,2,3}、再加个空集；

而真子集为{1}、{2}、{3}、{1,2}、{1,3}、{2,3}、再加个空集,不包括全集I本身.

非空真子集为{1}、{2}、{3}、{1,2}、{1,3}、{2,3},不包括I及空集.

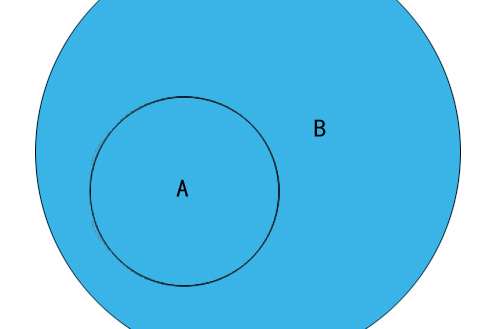
子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。

符号语言：若∀a∈A，均有a∈B，则A⊆B。