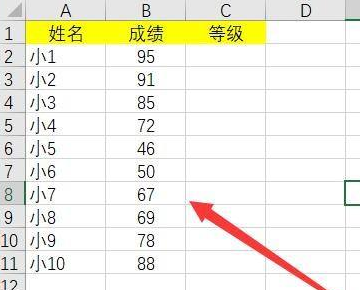
Simone已知函数
的有关信息介绍如下：
（1）f′(x)=ax-a=a(1x-x). 因为x>0,当a>0时,f(x)的单调增区间为(0,1), 单调减区间为(1,+∞); 当a<0时,f(x)的单调增区间为(1,+∞), 单调减区间为(0,1).（2）f′(2)=a/2-a=-a/2=tan45=1, a=-2 f(x)=-2lnx+2x-3,f′(x)=-2/x+2, g(x)=x^3+x^2(2-2/x+m/2)=x^3+(2+m/2)x^2-2xg'(x)=3x^2+(4+m)x-2 对于任意t∈[1,2],在区间(t,3)上不总是单调函数, ∴g′(x)在(2,3)上要有根g'(x)=0的两根x1x2=-2/3<0, ∴在(2,3)上只可能有一个根,还有个根小于0 ∴g′(2)g'(3)=(12+8+2m-2)(27+12+3m-2)=(18+2m)(37+3m)<0 ∴m的范围为-37/3
