最简单的勾股定理的证明方法是什么？

最简单的勾股定理的证明方法是什么？

证法一： 

这是最简单精妙的证明方法之一，几乎不用文字解释，可以说是无字证明。如图所示，左边是4个相同的直角三角形与中间的小正方形拼成的一个大正方形。

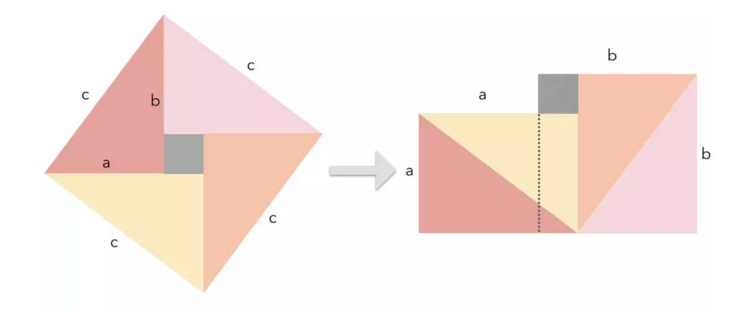
图形变换后面积没有变化，左边大正方形的边长是直角三角形的斜边c，面积是c2；右边图形可分割为两个正方形，它们的边长分别为直角三角形的两条直角边a和b，面积就是a2＋b2，于是a2＋b2＝c2。

图中左边的“弦图”最早出现在公元222年的中国数学家赵爽所著《勾股方圆图注》，赵爽是我国数学史上证明勾股定理的第一人。2002年8月，在北京召开的国际数学家大会，标志着中国数学进入崭新的时代，大会会徽就是这个“弦图”，寓意中国古代数学取得的重要成果。

证法二： 

这一解法应该是来历最有趣的证明方法之一，是由美国第20任总统茄菲尔德（JamesA.Garfield，1831～1881）用下图证明出的。

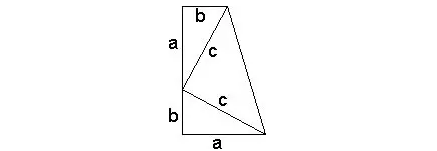
这位总统并不是一位数学家，他甚至都不曾学习过数学。他只是非正式地自学过几何知识，很喜欢摆弄基础图形，当他还是众议院议员时，想出了这个精巧的证明，1876年发表在《新英格兰教育杂志》(New England Journal of Education)上。总统先生的证明如下：

首先，图中的梯形面积为：

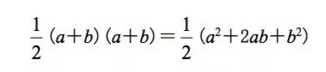
组成梯形的三个三角形的面积为：

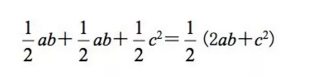
因此就有如下等式：

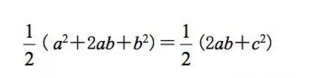
即得a2＋b2＝c2。  

接下来的两个证明非常简单易懂，被认为是所有证明中最短、最简单的证明，因为从开始到结束只用了几行。但这些证明依赖于相似三角形的概念，要全面展开这个概念还需要大量的基础工作，这里就不再赘述。

证法三：

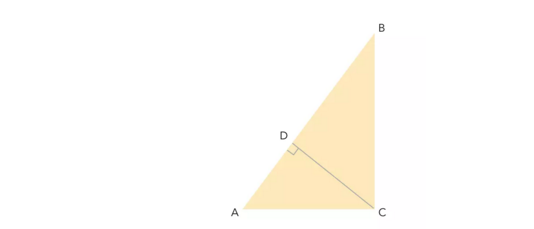
证法四： 

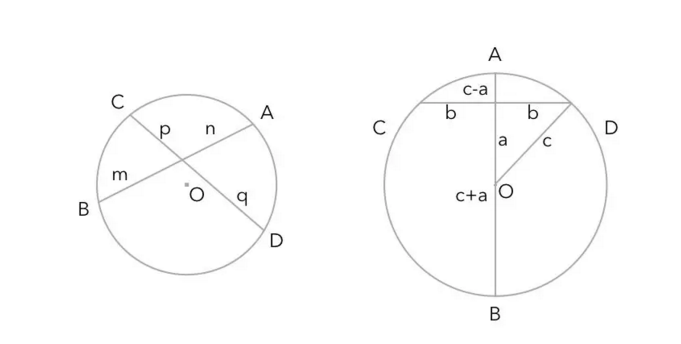
这一证法涉及到圆内相交弦定理：m·n＝p·q（如左图），再看AB和CD垂直的情况，相交弦定理仍然成立（如右图），因此(c－a)(c＋a)＝b2。即得c2－a2＝b2于是，a2＋b2＝c2。