正整数Z包不包括0

正整数Z包不包括0

正整数不包括0，整数包括正整数，负整数和零！

和整数一样，正整数也是一个可数的无限集合。在数论中，正整数，即1、2、3……；但在集合论和计算机科学中，自然数则通常是指非负整数，即正整数与0的集合，也可以说成是除了0以外的自然数就是正整数。正整数又可分为质数，1和合数。正整数可带正号（+），也可以不带。

正整数，为大于0的整数，也是正数与整数的交集。正整数又可分为质数，1和合数。正整数可带正号（+），也可以不带。如：+1、+6、3、5，这些都是正整数。 0既不是正整数，也不是负整数（0是整数）。

扩展资料：

以0为界限，将整数分为三大类：

1、正整数，即大于0的整数，如，1，2，3…

2、0既不是正整数，也不是负整数（0是整数）。

3、负整数，即小于0的整数，如，-1，-2，-3…。

任何一个满足下列条件的非空集合叫做正整数集合，记作N*。如果

Ⅰ、 1是正整数；

Ⅱ、 每一个确定的正整数a，都有一个确定的后继数a' ，a'也是正整数（数a的后继数a‘就是紧接在这个数后面的整数（a+1）。例如，1‘=2，2’=3等等。）；

Ⅲ 、如果b、c都是正整数a的后继数，那么b = c；

Ⅳ 、1不是任何正整数的后继数；

Ⅴ 、设S⊆N*，且满足2个条件（i）1∈S；（ii）如果n∈S，那么n'∈S。那么S是全体正整数的集合，即S=N*。(这条公理也叫归纳公理，保证了数学归纳法的正确性)

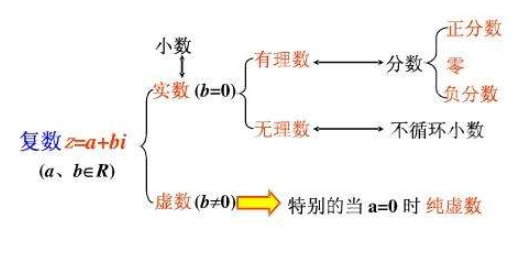
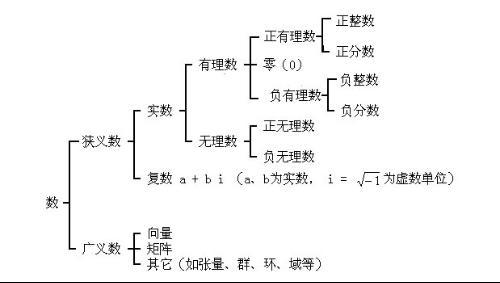
整数和分数统称有理数；无限不循环小数叫做无理数；有理数和无理数统称实数。全体实数的集合记为R，全体自然数的集合记为N，整数的集合记为Z。

规定了原点、正方向和单位长度的直线叫做数轴，每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都表示一个实数，实数和数轴上的点的这种一一对应的关系是数学中把数和形结合起来的重要基础。

负整数是小于0的整数；负整数与负整数的和仍为负整数；负整数与负整数的积为正整数；负整数存在最大值-1，不存在最小值；负整数在实数范围内不能开平方，不能开偶数次方，但是可以开奇数次方。

参考资料来源：百度百科——正整数