三门问题为什么是悖论？

三门问题为什么是悖论？

虽然该问题的答案在逻辑上并不自相矛盾，但十分违反直觉。

以下是蒙提霍尔问题的一个著名的叙述，来自 Craig F. Whitaker 于1990年寄给《展示杂志》（Parade Magazine）玛丽莲·沃斯·莎凡特（Marilyn vos Savant）专栏的信件：

“假设你正在参加一个游戏节目，你被要求在三扇门中选择一扇：其中一扇后面有一辆车；其余两扇后面则是山羊。你选择了一道门，假设是一号门，然后知道门后面有什么的主持人，开启了另一扇后面有山羊的门，假设是三号门。他然后问你：“你想选择二号门吗？”转换你的选择对你来说是一种优势吗？”

以上叙述是对Steve Selvin于1975年2月寄给American Statistician杂志的叙述的改编版本。 如上文所述，蒙提霍尔问题是游戏节目环节的一个引申；蒙提·霍尔在节目中的确会开启一扇错误的门，以增加刺激感，但不会容许参赛者更改他们的选择。如蒙提·霍尔寄给Selvin的信中所写：

“如果你上过我的节目的话，你会觉得游戏很快—选定以后就没有交换的机会。”

Selvin在随后寄给American Statistician的信件中（1975年8月）首次使用了“蒙提霍尔问题”这个名称。

一个实质上完全相同的问题于1959年以“三囚犯问题”（three prisoners problem）的形式出现在马丁·加德纳（Martin Gardner）的《数学游戏》专栏中。加德纳版本的选择过程叙述得十分明确，避免了《展示杂志》版本里隐含的前提条件。

这条问题的首次出现，可能是在1889年约瑟夫·贝特朗所著的 Calcul des probabilités 一书中。 在这本书中，这条问题被称为“贝特朗箱子悖论”（Bertrand's Box Paradox）。

假设

Mueser 和 Granberg 透过厘清细节，以及对主持人的行为加上明确的介定，提出了对这个问题的一种不含糊的陈述︰

1、 现在有三扇门，只有一扇门有汽车，其余两扇门的都是山羊。

2、 汽车事前是等可能地被放置于三扇门的其中一扇后面。

3、 参赛者在三扇门中挑选一扇。他在挑选前并不知道任意一扇门后面是什麽。

4、 主持人知道每扇门后面有什么。

5、 如果参赛者挑了一扇有山羊的门，主持人必须挑另一扇有山羊的门。

6、 如果参赛者挑了一扇有汽车的门，主持人等可能地在另外两扇有山羊的门中挑一扇门。

7、 参赛者会被问是否保持他的原来选择，还是转而选择剩下的那一扇门。

转换选择可以增加参赛者拿到汽车的机会吗？

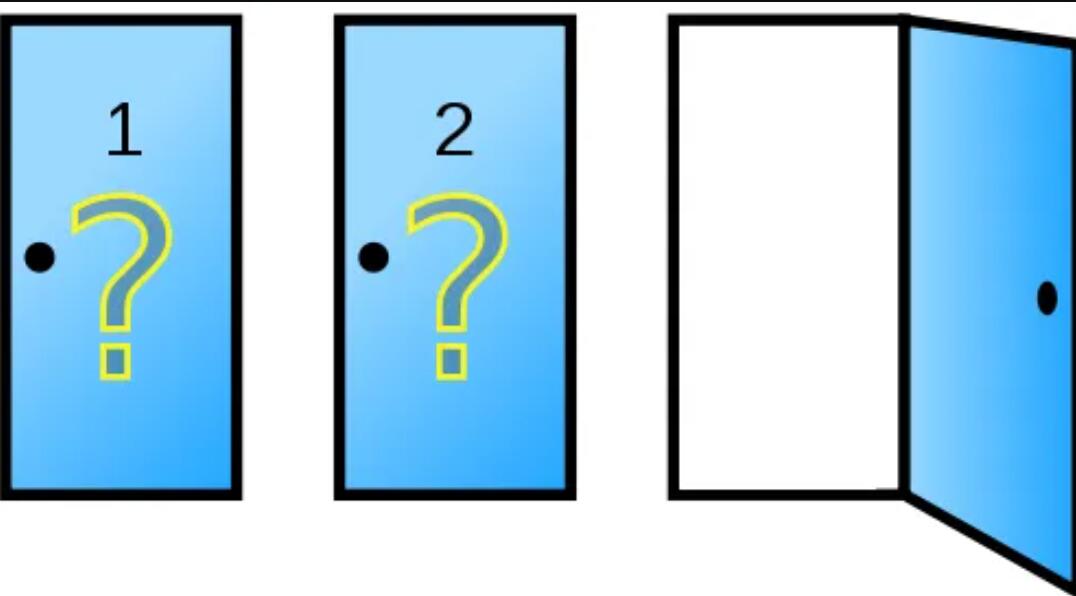
解答

有三种可能的情况，全部都有相等的可能性（1/3）：

参赛者挑汽车，主持人挑两头羊的任何一头。变换将失败。

参赛者挑A羊，主持人挑B羊。变换将赢得汽车。

参赛者挑B羊，主持人挑A羊。变换将赢得汽车。

问题是：关于第一种可能性的表述可以分成两种可能吗？

参赛者挑汽车，主持人挑A羊。变换将失败。

参赛者挑汽车，主持人挑B羊。变换将失败。

在后两种情况，参赛者可以透过变换选择而赢得汽车。第一种情况是唯一一种参赛者透过保持原来选择而赢的情况。因为三种情况中有两种是透过变换选择而赢的，所以透过变换选择而赢的概率是2/3。

如果没有最初选择，或者如果主持人随便打开一扇门（可能主持人会直接开到汽车门，导致游戏结束），又或者如果主持人只会在参赛者作出特定选择某一门时才会问是否变换选择的话，问题都将会变得不一样。例如，如果主持人先从两只山羊中剔除其中一只，然后才叫参赛者作出选择的话，选中的机会将会是1/2。

还可以用逆向思维的方式来理解这个选择。无论参赛者开始的选择如何，在被主持人问到是否更换时都选择更换。如果参赛者先选中山羊，换之后百分之百赢；如果参赛者先选中汽车，换之后百分之百输。而选中山羊的概率是2/3，选中汽车的概率是1/3。

所以不管怎样都换，相对最初的赢得汽车仅为1/3的机率来说，转换选择可以增加赢的机会。

以上内容参考 百度百科-三门问题