三角恒等变换公式是什么?

三角恒等变换公式是什么?

三角恒等变换是一组用于改写三角函数表达式的公式。它们可以将一个三角函数表达式转化为等价的、但形式上不同的表达式，从而简化计算或证明过程。以下是常见的三角恒等变换公式：

1. 余弦的平方与正弦的平方和差公式：

cos²(x) + sin²(x) = 1

cos²(x) - sin²(x) = cos(2x)

sin²(x) - cos²(x) = -cos(2x)

2. 余弦和正弦的和差公式：

cos(x ± y) = cos(x) * cos(y) ∓ sin(x) * sin(y)

sin(x ± y) = sin(x) * cos(y) ± cos(x) * sin(y)

3. 正切和余切的和差公式：

tan(x ± y) = (tan(x) ± tan(y)) / (1 ∓ tan(x) * tan(y))

cot(x ± y) = (cot(x) * cot(y) ∓ 1) / (cot(y) ± cot(x))

4. 二倍角公式：

sin(2x) = 2 * sin(x) * cos(x)

cos(2x) = cos²(x) - sin²(x) = 2 * cos²(x) - 1 = 1 - 2 * sin²(x)

tan(2x) = (2 * tan(x)) / (1 - tan²(x))

5. 半角公式：

sin(x/2) = ± sqrt((1 - cos(x)) / 2)

cos(x/2) = ± sqrt((1 + cos(x)) / 2)

tan(x/2) = ± sqrt((1 - cos(x)) / (1 + cos(x)))

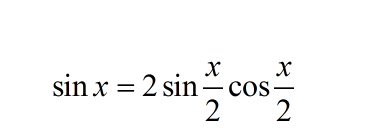
这些是常见的三角恒等变换公式，它们在解三角方程、化简三角函数表达式和证明三角恒等式等情况下非常有用。需要根据具体的问题选择合适的公式进行应用。

三角恒等变换公式在解决三角函数相关的问题中有广泛的应用

1. 化简三角函数表达式：

通过应用三角恒等变换公式，可以将复杂的三角函数表达式简化为更简单的形式，便于计算和分析。例如，可以利用和差公式将一个三角函数的和、差表示为乘积形式，或者利用平方和差公式将三角函数的平方项合并。

2. 证明三角恒等式：

利用三角恒等变换公式，可以推导出新的三角恒等式。通过对已知的三角恒等式进行代换、化简和变形，可以得到新的恒等式，从而丰富了我们对三角函数关系的理解。

3. 解三角方程：

在解三角方程时，可以使用三角恒等变换公式将方程转化为等价但更简单的形式。通过转化后的方程，可以更容易地求解未知数。

4. 凑项与消项：

当在数学计算或证明过程中需要凑项或消项时，三角恒等变换公式可以派上用场。通过适当选择和应用恒等变换公式，可以实现凑项或消项的目的，使得计算或证明更加简洁和高效。

5. 证明三角形的性质：

三角恒等变换公式可以用于证明三角形的各种性质。例如，利用三角恒等变换公式可以证明等边三角形的角度相等、直角三角形的勾股定理等。

三角恒等变换公式例题

例题1：证明恒等式 sin(x) * cos(x) = sin(2x) / 2.

解析：

我们可以利用二倍角公式 sin(2x) = 2 * sin(x) * cos(x)，将 sin(2x) 代入恒等式中，得到：

sin(x) * cos(x) = (2 * sin(x) * cos(x)) / 2

= sin(2x) / 2

因此，恒等式成立。

例题2：求证恒等式 tan(x) + cot(x) = sec(x) * csc(x).

解析：

我们可以利用正切和余切的定义以及三角恒等变换公式进行证明：

tan(x) + cot(x) = sin(x)/cos(x) + cos(x)/sin(x)

= (sin^2(x) + cos^2(x))/(sin(x)*cos(x))

= 1/(sin(x)*cos(x))

= 1/((1/csc(x))*(1/sec(x)))

= sec(x)*csc(x)

因此，恒等式成立。

这些例题展示了如何使用三角恒等变换公式进行证明或运算。通过应用适当的恒等变换公式，我们可以将复杂的三角函数表达式化简为更简单的形式，从而得到结论或简化计算过程。