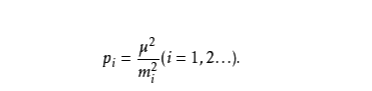求三角形面积的海伦公式是什么？

求三角形面积的海伦公式是什么？

假设有一个三角形，边长分别为a、b、c，三角形的面积S可由以下公式求得： S=\sqrt{s(s-a)(s-b)(s-c)} 而公式里的s： s=\frac{a+b+c}{2} 由于任何n边的多边形都可以分割成n-2个三角形，所以海伦公式可以用作求多边形面积的公式。比如说测量土地的面积的时候，不用测三角形的高，只需测两点间的距离，就可以方便地导出答案。 [编辑]证明 与海伦在他的着作"Metrica"中的原始证明不同，在此我们用三角公式和公式变形来证明。设三角形的三边a、b、c的对角分别为A、B、C，则馀弦定理为 \cos(C) = \frac{a^2+b^2-c^2}{2ab} 从而有 \sin(C) = \sqrt{1-\cos^2(C)} = \frac{ \sqrt{-a^4 -b^4 -c^4 +2a^2b^2 +2b^2c^2 +2c^2a^2} }{2ab} 因此三角形的面积S为 S = \frac{1}{2}ab \sin(C) = \frac{1}{4}\sqrt{-a^4 -b^4 -c^4 +2a^2b^2 +2b^2c^2 +2c^2a^2} = \sqrt{s(s-a)(s-b)(s-c)} 最后的等号部分可用因式分解予以导出。